Red de un prisma regular de base triangular Curriculum Nacional. MINEDUC. Chile.

Fórmulas del volumen de un prisma triangular regular e irregular. El volumen del prisma triangular es el producto del área de de una de las bases por la altura.. Jesús, la fórmula del volumen de cualquier prisma es: Volumen = Area de la base x altura. si cual es la formula no entendi lo de arriba. Respuestas. 15 junio, 2018 a las 07:21.
Volumen de un Prisma Triangular Fórmulas y Ejercicios Neurochispas
Como un poliedro semirregular (o uniforme) Un prisma triangular recto es semirregular o, más generalmente, un poliedro uniforme, si las caras de la base son triángulos equiláteros, y las otras tres caras son cuadrados.Se puede ver como un hosoedro trigonal truncado, representado por un símbolo de Schläfli t{2,3}. De otra manera, puede verse como el producto cartesiano de un triángulo y.
Decaedros Prisma de base triangular
Área de un prisma triangular regular. El prisma triangular regular es aquel que tiene como bases dos triángulos equiláteros.Sus caras laterales son rectángulos iguales.. El área de las bases se calcula mediante la fórmula del área de triángulo equilátero (A b), mientras que el área lateral es el resultado de multiplicar el perímetro de la base (P b) por la altura (h) del prisma.
Calcular el área de un prisma triangular. Calcular la superficie de un prisma triangular. YouTube

Características de un prisma triangular. Sus bases son dos triángulos idénticos y paralelos. Tiene un total de 5 caras, 2 caras de las bases y 3 caras laterales. Tiene 3 caras laterales en forma de rectángulos (paralelogramo) que unen las 2 bases. Tiene un total de 6 vértices, que son los puntos donde concurren las caras del prisma.
Formula De Area De Un Prisma Triangular / Formula Para Obtener El Area Y El Volumen De Un Prisma

Características principales de un prisma triangular. Las siguientes son algunas de las características más importantes de los prismas triangulares: Tienen un total de 9 aristas. Tienen un total de 5 caras. Tienen un total de 6 vértices. Tienen dos caras triangulares, llamadas bases y tres caras rectangulares, llamadas caras laterales.
EL PROFE LÓPEZ PRISMAS

Prisma Triangular Prismas Cuadrangulares Prismas Pentagonales Desarrollo de un Prisma Recto. El Desarrollo lateral de un Prisma Recto es un rectángulo. La longitud de su base es el perímetro de la base del mismo, y su altura, la altura de este. Si lo cortamos a lo largo de algunas de sus aristas, lo abrimos y ponemos las caras sobre un plano.
Prisma triangular ¿Qué es? 5 Características, Área y Volumen
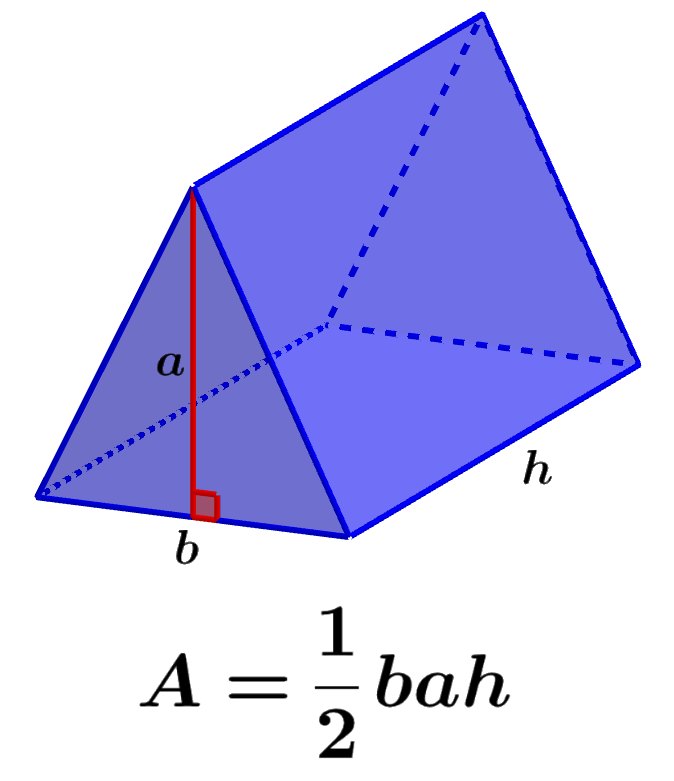
Entonces, podemos usar la siguiente fórmula para calcular el volumen de un prisma triangular: V=\frac {1} {2}b\times a\times h V = 21b × a× h. en donde, b es la longitud de la base del triángulo. a es la longitud de la altura del triángulo. h es la longitud de la altura del prisma.
Volumen Prisma Triángular YouTube

El área superficial de los prismas triangulares puede ser calculada al sumar las áreas de cada una de las caras del prisma. Sabemos que el área de un triángulo es igual a un medio de la base por la altura, por lo que el área de ambas bases es igual a ba. El área de cada una de las caras rectangulares es igual a la longitud del rectángulo.
Como Se Calcula El Volumen De Un Prisma Triangular rowrich

Esta es la ecuación básica del volumen de un prisma triangular: Volumen = 1/2 × Base × Altura × Longitud. Donde: Base y Altura son los valores de la cara triangular del prisma; Longitud es la longitud de todo el prisma, es decir, la distancia entre dos caras. Triángulo rectángulo.
¿Cuántos vértices tiene un prisma triangular? Prismás triangulares

Coloca ese número en el lugar de la fórmula. [5] Por ejemplo, la fórmula ahora quedará así . 3. Multiplica el área triangular por la altura del prisma para encontrar el volumen. Ahora que tienes todas las partes de la ecuación, multiplica el área por la altura. El resultado será el volumen del prisma triangular.
Prisma triangular ¿Qué es? 5 Características, Área y Volumen
Elementos del prisma triangular. En un prisma triangular se pueden diferenciar los siguientes elementos: . Bases (B): son dos triángulos paralelos e iguales.; Caras (C): los tres paralelogramos de las caras laterales y las dos bases. Tiene cinco caras. Altura (h): distancia entre las dos bases del prisma.En el caso del prisma recto la longitud de la altura h y la de las aristas de las caras.
PRISMA Clasificación y Características Aulaprende
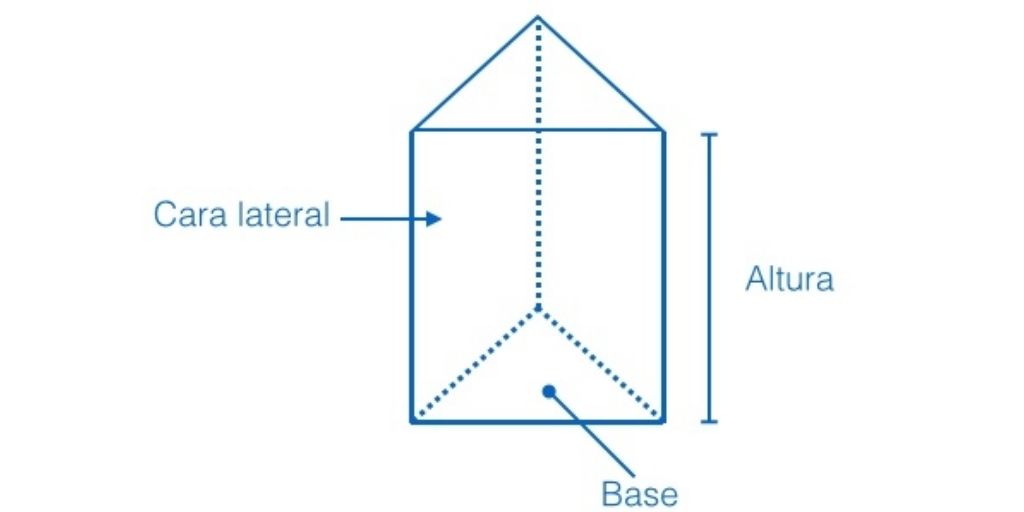
Determina la altura del prisma: La altura del prisma es la distancia perpendicular entre las dos bases paralelas. Multiplica el área de la base por la altura. Fórmula específica para el prisma triangular: V = (b t · h t / 2) · h p. Donde: V es el volumen del cuerpo geométrico. b t es la base del triángulo de una de sus bases.
Formula De Area De Un Prisma Triangular / Area De Superficie De Prismas Triangulares Ck 12

Las bases de un prisma triangular o prisma triangular recto, son en realidad dos triángulos que podemos encontrar a cada lado del prisma. Estos dos triángulos son siempre iguales. Además, ellos pueden ser cualquier tipo de triángulo. Repasemos los tipos de triángulos que conocemos: Triángulo equilátero. Triángulo isósceles.
Prisma triangular ¿Qué es? 5 Características, Área y Volumen
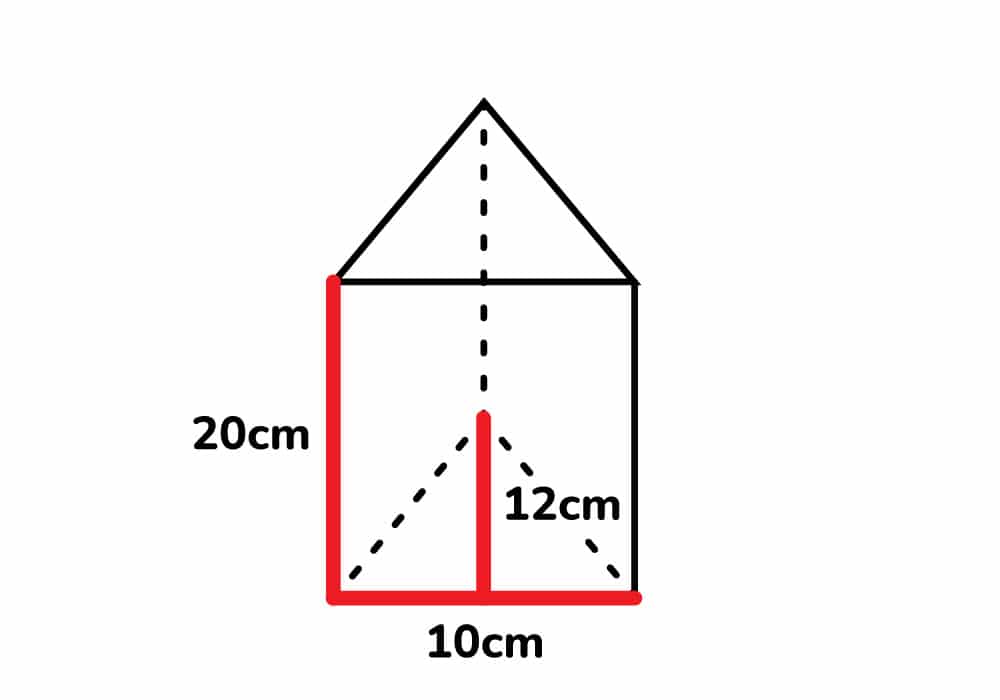
Utiliza la fórmula para el volumen de un prisma triangular y de un cubo para resolver algunos problemas de geometría de sólidos.. que es un cuadrado del cual salen cuatro triángulos o bien está la pirámide con base triangular hay varias ahorita no quiero confundirte solo quiero decirte que hay varias figuras que involucran triángulos.
Volumen del prisma recto Ejemplo 4 base triangular YouTube

El volumen de un prisma triangular se calcula multiplicando el área del triángulo de la base por la altura del prisma. Y, en concreto, el volumen de un prisma triangular regular es igual al cuadrado de la longitud de la base, por la altura del prisma triangular por la raíz de tres partido por cuatro. De modo que la fórmula para calcular el.
Geometría del espacio. Prismas Escolar ABC Color

V = 157.5 cm3. La respuesta es que el volumen de este prisma triangular es 157.5 cm3. Ejemplo 9.15.5. Cuál es el volumen de un prisma triangular con las siguientes dimensiones: b = 4 mmh = 3 mmh = 5 mm. Solución. Primero, conecte los valores para la fórmula de área de un triángulo para encontrar el área base, B.
.

